"La vista ci fa conoscere più di tutte le altre sensazioni e ci rende manifeste numerose differenze fra le cose", scrive Aristotele nella prima pagina della sua Metaphysica (A 1 980a24-26), l'opera che più di tutte lo consegna ai vertici del pensiero classico. Altrove, in un'opera forse meno conosciuta ma contente la sintesi di ciò che lo Stagirita intendeva per scienza, gli Analitici Secondi, si legge che "sapere è il conoscere mediante dimostrazione" (I 2 71b18), affermazione che viene meditata, approfondita e compresa appieno nel corso di tutta la trattazione. Sono i due corni del dilemma su come si debbano effettuare la conoscenza e il sapere: se mediante il ricorso ai sensi e in particolare al primo tra essi, la vista, o se mediante la mediazione della dimostrazione così come intesa da Aristotele, cioè assiomatico-deduttiva.

Certo è che l'idea di "dimostrazione" non fu inventata da Aristotele; tanto meno fu inventata da Euclide, nonostante la sua celebrità lo abbia consegnata alla storia come simbolo della matematica greca e nonostante le dimostrazioni degli Elementi abbiano rappresentato per secoli il modello di riferimento. Poter dimostrare significa possedere un sapere certo e incontrovertibile: il rigore logico delle deduzioni è ciò che sembra procurare la conquista di questo sapere. Eppure sfogliando gli Elementi si ha la sensazione che si incominci con la preponderanza di una geometria "per immagini semplici" (geometria piana, libri I-IV), fino ad approdare ad una geometria fatta di "oggetti più complessi" (geometria solida e poliedri, libri XI-XIII); come se si iniziasse da dimostrazioni più "visibili" fino a dimostrazioni di più difficile comprensione, nelle quali è necessaria l'astrazione formale e il rigore deduttivo.

Secondo Szabó, l'idea di "dimostrazione matematica" distingue profondamente la matematica pre-ellenica e quella ellenica¹. Von Fritz sostiene che proprio per riuscire a distinguere tra i tanti risultati esatti e inesatti della matematica orientale, i Greci "dovettero crearsi nuove basi. Di qui il bisogno di dare di tutto, ma soprattutto degli enunciati più elementari, una dimostrazione esatta, non importa come"².

Ma quali caratteristiche dovesse avere la "dimostrazione matematica", se fosse possibile formulare delle regole per rendere la procedura dimostrativa sempre più rigorosa, trasmissibile, utilizzabile devono essere state le domande che hanno dato origine ad un lungo dibattito, visto che i primi tentativi di dimostrazione inizialmente richiamati hanno caratteristiche diverse dalla nostra idea preconcetta di "dimostrazione" (che, chiaramente, è di sapore aristotelico-euclideo). Non è neanche da escludere l'ipotesi che ogni singolo pensatore si organizzasse come poteva, proponendo tipi di dimostrazioni molto diversi fra loro.

Sempre Von Fritz ha distinto nella scienza greca il procedere per epagoge dal procedere per apagoge, ad indicare due diverse vie praticate dagli antichi greci per dimostrare, prima che si configurasse come via regia la forma deduttiva data alla dimostrazione da Aristotele ed Euclide. Epagoge letteralmente significa "accostamento", ovvero un metodo in cui per verificare determinate proprietà vengono "avvicinati" gli oggetti matematici in discussione, quasi per facilitare la presa visione di quel passaggio logico e poter poi passare al successivo o addirittura alla conclusione. Apagoge³, che letteralmente indica l'atto di allontanare, è il metodo indiretto di riduzione: "allontanare" poiché nel processo dimostrativo si allontana un'ipotesi per dimostrare quella opposta, e lo si fa lavorando esclusivamente su concetti astratti, senza ricorrere costantemente all'intuizione e all'evidenza come nell'epagoge.

La compresenza di queste due tendenze, che in modo indicativo potremmo anche chiamare "tendenza al concreto" e "tendenza all'astratto", si ritrovano costantemente nel primo pensiero matematico greco: capire come sia stato possibile farle convivere oltre che un problema teoretico, è anche un problema di precise origini storiche.

L'uso della figura e di meccanismi pratici nelle prime dimostrazioni della matematica greca

Un fondazionalista accorderebbe il giudizio platonico verso quanti "in modo ridicolo [...], parlano sempre di disegnar quadrati, di costruire figure e di sommarle fra loro, […] mentre tutta questa disciplina andrebbe sviluppata in vista della conoscenza" (Repubblica 527A-B): tali parole sono la prova che l'idea di non introdurre figure nella dimostrazione, in modo da eliminare qualsiasi ricorso all'intuizione, è perseguita fin nei nostri tempi⁴.

C'è un aspetto dell'uso della figura che è direttamente connesso con quanto sottolineava Aristotele sul valore della vista nella costruzione del sapere. Osservare la figura permette di comprendere più velocemente quale problema stiamo cercando di risolvere o quale è addirittura la soluzione al problema. Ma mentre l'intuizione fa cogliere l'oggetto immediatamente e in modo indistinto, la figura comporta già una mediazione: rappresentare l'oggetto significa fare una inferenza, non deduttiva ma pur sempre un'inferenza e per di più ampliativa, poiché significa estrapolare qualcosa che non è contenuto propriamente nell'oggetto⁵.

Dunque, tra uso della figura e ricorso all'intuizione c'è differenza, nonostante il loro legame sia strettissimo; ma l'uso della figura rimanda anche all'aspetto pratico che intercorre nella costruzione della conoscenza. Tale uso dovette essere anche sistematico in molti casi: Netz ha mostrato l'interdipendenza tra l'uso di figure (diagramma) e il testo in Apollonio⁶. Ma ci sembra che ciò accadeva già molto prima di Apollonio: l'esame della tradizione papirologica greca sulle figure, nonostante non sia ancora studiata sistematicamente, ammette che il ricorso a righelli, squadre e compassi fosse usuale per la rappresentazione di oggetti bidimensionali e di alcuni oggetti tridimensionali, nonostante in quest'ultimo caso spesso si rappresentasse separatamente la parte non visibile; più delicata è la questione della rappresentazione degli oggetti tridimensionali di cui si cerca di dare comunque una rappresentazione figurale diretta, che però a volte sembra più di tipo pittorico e meno tecnico. Se questa può sembrare una questione oziosa, in realtà è di una certa importanza poiché significa capire fino a che punto le figure volessero rappresentare oggetti reali, magari riproducendoli in scala, o fino a che punto invece le figure fossero utilizzate in modo molto più informale. Ed in effetti sappiamo che tentativi di ritrarre il mondo erano stati compiuti da Erodoto, che sa descrivere ammirevolmente bene, con parole, il Nord Africa (ad es., Hdt. II 11, 12); inoltre Strabone ci informa che tentativi di rappresentarsi la totalità del mondo erano stati già compiuti da Anassimandro ed Ecateo mediante la compilazione di carte geografiche (D.-K. 12A6); e che sia Anassimandro che Anassimene si avvalsero di modelli grafici per descrivere l'universo (la colonna, il piatto: D.-K. 12A11(3); D.-K. 13A20, B2a). Netz ipotizza si usassero figure "pittoriche" in ambiente privato, quando si discuteva dei risultati ottenuti dai matematici⁷; se questa è una tesi valida, si potrebbe anche pensare che viceversa le immagini pittoriche di oggetti tridimensionali stimolasse la formulazione di problemi matematici, quasi in senso costruttivista.

Un problema ancora più grave dell'impiego di figure nelle dimostrazioni è quello del ricorso ad espedienti pratici: doveva esserci l'uso avvalso di dimostrare "mostrando" che tecnicamente e praticamente una certa cosa era possibile, altrimenti non si giustificherebbe il rimprovero rivolto da Platone ai suoi allievi Eudosso, Menecmo e Anfinomo "i quali volevano ridurre il problema della duplicazione dei volumi su apparati strumentali e meccanici (…) a portata solamente pratica"; così facendo essi distruggevano la geometria, riducendola a cosa sensibile anziché facendola partecipare alle cose eterne e immutabili (12 D1e, Lasserre⁸). Dimostrare una proposizione geometrica magari costruendo nella realtà un modello tridimensionale per osservarlo, sezionarlo, rovesciarlo e così via è più che mai una soluzione da includere nell'ambito della matematica "pratica"; addirittura potrebbe far venir pure il dubbio se considerare questo genere di esercizio "matematico".

L'alternativa che allora si pone è se adottare un preciso concetto di "dimostrazione" (che in ultima analisi è di sapore aristotelico-euclideo) e dunque tagliar fuori da esso molti casi di dimostrazioni pre-euclidee di carattere essenzialmente pratico; oppure partire dai dati storici e riadattare, riformulare il concetto di "dimostrazione" nella scienza pre-euclidea.

Recentemente, rispondendo a Netz, Giardina propone l'idea di uno sviluppo "graduale" della matematica deduttiva; per lo studioso americano si potrebbe parlare di "matematica greca" solo in relazione al prototipo aristotelico-euclideo⁹. Ma questo atteggiamento porterebbe ad escludere che anche una matematica neopitagorica o neoplatonica possano essere "vere" matematiche¹⁰.

Inizieremo allora proprio da alcune di quelle dimostrazioni oggetto di perplessità, nella convinzione che possano invece suggerirci molto di questo antico orizzonte matematico. Senza valutazioni svolte secondo il concetto di "dimostrazione" rielaborato in seguito, l'evidenza testuale fa riemergere dati della matematica di VI-V secolo su cui non possiamo sorvolare, ma che vanno capiti e storicizzati: solo alla fine potremo provare a concludere su cosa inizialmente si intendesse per "dimostrazione".

Le prime dimostrazioni

La centralità dell'esperienza diretta e dell'osservazione delle figure si rintraccia in dati storici che non sono "dimostrazioni", ma sono comunque indice di questo riferimento al pratico: la classificazione pitagorica dei numeri in numeri triangolari e numeri quadrati può essere in una certa misura così intesa, ponendo in stretta correlazione numeri e figure¹¹. Così anche la storia del termine "gnomone", che dapprima è uno strumento astronomico, poi uno strumento per disegnare angoli retti; in seguito diviene quella figura da aggiungere affinché un quadrato dia luogo ad un quadrato più grande (Aristotele¹²) fino ad essere in Euclide¹³ quella figura da aggiungere per dar luogo ad un qualsiasi parallelogramma; infine in Erone (Def. 58) lo gnomone viene ad essere un numero o una figura da aggiungere a un numero o ad una figura per produrre qualcosa di simile e di più grande¹⁴. L'aspetto pratico e teorico sono addirittura indistinguibili.

La prima dimostrazione matematica di cui gli antichi fanno menzione risale a Talete di Mileto, del quale riferisce Proclo: "dicono che sia stato il famoso Talete il primo a dimostrare che il cerchio è bisecato dal diametro. (…) Se si vuol dimostrare il fatto per via matematica, immaginiamo condotto il diametro e sovrapposta una parte del cerchio all'altra" (Comm. a Eucl. 157.10 = D.-K. 11A20¹⁵). Se uno dei due semicerchi, continua Proclo, fosse minore dell'altro, le due semicirconferenze dovrebbero avere i raggi disuguali; ma ciò è impossibile, dunque esse sono uguali, al pari dei relativi semicerchi, e il diametro biseca il cerchio.

Su questa testimonianza si sono sollevate più obiezioni circa l'uso del termine "dimostrò" (apodeixai). Secondo Zeuthen, Hankel¹⁶, Heath¹⁷, Frajese¹⁸ probabilmente si trattava di una sorta di prova pratica, fatta magari concretamente dividendo in due parti un cerchio realizzato in un qualche materiale e poi sovrapponendole. Questo tipo di procedura poteva essere diffusa al tempo, magari impiegata in lavori pratici e indicata come "dimostrazione": quindi in quel "dimostrò" non va visto qualcosa di particolarmente innovativo o sorprendente.

Anche Tannery¹⁹, Hankel²⁰ e Heath²¹ di nuovo esprimono delle perplessità sul senso di questa "dimostrazione", basate sul fatto che lo stesso Euclide ne fa una definizione (I def.17: "diametro del cerchio è una retta condotta per il centro e terminata da ambedue le parti dalla circonferenza del cerchio, la quale retta taglia anche il cerchio per metà"), evitando di dimostrarla.

Ma abbiamo detto che è proprio questo il senso da cogliere: cosa significasse "dimostrare" e come il significato originario evolse in quello più definito e ricco di connotazione che troviamo in Euclide. Certo Talete non intendeva per "dimostrazione" quello che poteva intendere Euclide; inoltre Euclide sistema tra le definizioni ciò che veniva considerato "dimostrato" appunto semplicemente perché "mostrato". Il fatto che ricorresse ad un meccanismo pratico significa affidarsi all'evidenza e da lì trarre una conclusione generale di carattere teorico²².

In questo senso già M. Cantor considerava seriamente possibile che Talete avesse preso spunto dall'aspetto di certe figure circolari divise in un numero di settori equivalenti da 2, 4 o 6 diametri, rappresentate in alcuni monumenti egiziani o sui vessilli portati dai re tributari asiatici sotto la XVIII dinastia²³. Ragionando su queste figure avrebbe ideato la sua "dimostrazione", che a diritto può essere chiamata in questo modo.

In ogni caso, che Talete si sia potuto mettere a "mostrare" per sovrapposizione la congruenza dei due semicerchi ottenuti spezzando realmente lungo il diametro una tavoletta circolare (ad esempio di legno), già sarebbe significativo: esprimerebbe la volontà di capire fino in fondo, di verificare ricorrendo ad un espediente pratico ciò che intuitivamente sembra vero, di sottoporre a controllo una conoscenza istintivamente data per certa. Non solo senza questo desiderio preliminare, la dimostrazione scientifica non sarebbe mai potuta nascere; ma significa proprio che inizialmente il dato empirico rivestiva un ruolo centrale, poiché ad esso si demandava la valutazione definitiva sul dato intuitivo.

D'altronde lo stesso Talete ci fornisce indizi per pensare che proprio questo atteggiamento produsse le prime importanti conquiste, che destarono stupore già nell'antichità: Plutarco ci ricorda infatti l'ammirazione del re Amasi vedendo che il Milesio era riuscito a trovare un metodo generale con cui misurare l'altezza di una piramide (D.-K. 11A20), segmento che sfugge ad una misurazione diretta e che richiede un ragionamento indiretto per il calcolo, e lo avrebbe fatto usando l'ombra proiettata da un bastone.

Lo stupore cui Plutarco allude è comprensibile: pensare di ricorrere ad una grandezza misurabile (l'ombra proiettata dal bastone) per determinare la misura di un'altra grandezza inaccessibile (l'altezza della piramide) è un'idea estremamente interessante ed evidentemente nessuno fino ad allora ci aveva pensato. Per capire però la fattività della procedura di Talete è necessario approfondire il problema da un punto di vista geometrico.

Chiamando D l'estremo dell'ombra, non ha senso calcolarne la distanza dal lato di base (cioè ID), perché non è quello il segmento equivalente all'altezza del monumento. Il segmento che cerchiamo è HD, equivalente al segmento inaccessibile GH: come misurarlo?
 
 

AC: bastone
GH: altezza della piramide

Poiché Plutarco chiama in causa l'idea di proporzione, che sicuramente Talete non possedeva in forma raffinata²⁴, conviene rifarsi alle testimonianze di Plinio e Diogene Laerzio per avanzare delle ipotesi:

Plin. N. H. XXXVI 82 (= D.-K. 11A21): "Talete di Mileto riuscì a determinare la misura dell'altezza delle piramidi, misurandone l'ombra nel momento in cui suole essere pari al corpo che la proietta".

D.L. I 27 (=D.-K. 11A1): "Ieronimo [di Rodi, n.d.a.] dice che misurò anche l'altezza delle piramidi dall'ombra, avendo osservato quando la nostra ombra ha la stessa altezza del corpo".

Assumiamo allora che Talete abbia misurato l'ombra proiettata dalla piramide in un preciso giorno e ora dell'anno, esattamente allorché l'ombra di un oggetto qualsiasi, al mezzogiorno della latitudine in questione, è lunga quanto l'altezza dell'oggetto. Per determinare il momento esatto in cui operare Talete avrebbe semplicemente confrontato la lunghezza di un bastone (AC) e l'ombra da esso proiettata sul terreno (BC). Misurando la lunghezza dell'ombra della piramide in quell'istante, e sfruttando la particolare orientazione delle piramidi da sud a nord, Talete avrebbe potuto risalire alla misura dell'altezza della piramide, vediamo come. Detto H il piede dell'altezza, che cade esattamente al centro del quadrato di base²⁵, il segmento HD è equivalente al segmento inaccessibile GH (GH = HD), e somma a sua volta del segmento pure inaccessibile HI più il segmento misurabile ID. Ma HI vale manifestamente la metà del lato della piramide, un dato quindi misurabile dall'esterno, e il gioco è fatto.

È verosimile che Talete abbia potuto lavorare su un modello di piramide, ragionando sul quale avrebbe cercato di capire come trovare il segmento EF, equivalente all'altezza GH non misurabile. Avrebbe cioè ricostruito la situazione per renderla "sperimentabile" e studiarla a fondo. Si sarebbe quindi accorto della possibilità di costruire il quadrato HDEF equivalente al quadrato di base della piramide, abilità commisurabile alle conoscenze geometriche di quei tempi in quanto non presuppone altro che la padronanza delle proprietà della semplicissima figura del quadrato e la capacità di riprodurla sul terreno. Ma è indubbio che tutta la rielaborazione teorica prende spunto dall'osservazione concreta e che probabilmente si svolgeva mediante modelli disegnati o appositamente costruiti²⁶.

Ma arrivando alla metà del V sec., un'altra attestazione del sistematico ricorso alle figure nella dimostrazione ci viene fornito dalla questione della quadratura delle lunule, notoriamente di proprietà di Ippocrate di Chio²⁷, autore anche dei primi Elementi (D.-K. 42A1). La quadratura delle lunule o metodo dei segmenti²⁸ - si sa - trova spazio nella ricerca del più generale problema della quadratura del cerchio, uno dei problemi speciali la fama dei quali arrivava fin nelle arene, se addirittura Aristofane ne faceva parlare ai suoi personaggi²⁹. Quadrare una lunula significa trovare una superficie poligonale piana equivalente (e dunque dall'area più facilmente calcolabile), in modo da ottenere indirettamente anche la misura della superficie della grandezza curvilinea.

Simplicio ci riporta il resoconto che della dimostrazione di Ippocrate offriva la perduta Storia delle geometria di Eudemo; una dimostrazione considerata generale poiché valevole nei casi in cui l'arco esterno della lunula è pari, minore o maggiore di una semicirconferenza. Il primo caso è quello in cui l'arco esterno è pari ad una semicirconferenza. Il caso è particolarmente interessante ai nostri scopi poiché la dimostrazione viene svolta dichiaratamente mediante il ricorso ad una figura (apedidou…perigrapsas, da Simplicio, ad. h. l. 60, 22 61-62), cioè "circoscrivendo" un semicerchio intorno ad un triangolo rettangolo isoscele e costruendo sulla base un segmento circolare simile a quelli tagliati fuori dai lati del triangolo" (ibid. 59-64). La seguente figura, utilizzata per la dimostrazione, manca nei codici ed è stata riprodotta solo dall'edizione Diels, apportando delle aggiunte per facilitare la comprensione³⁰.
 
 

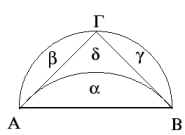
Al ragionamento svolto sul disegno, Eudemo premette la proposizione per cui segmenti circolari simili stanno fra loro come i quadrati delle loro basi [A]³¹, provata in base all'ulteriore principio per cui i quadrati dei diametri stanno fra loro come i loro circoli [B]; un'altra premessa è che segmenti simili comprendono anche angoli uguali, per cui deriva che l'angolo in un semicerchio è retto.

Da qui si procede sulla figura. Dal disegno risulta chiaro che la lunula in questione (b +d +g ) risulta uguale al triangolo ABG . Infatti, applicando il teorema di Pitagora esteso alle lunule (presupponendo le proposizioni date), si ha . Quindi:
 
 

Anche la dimostrazione del caso in cui la lunula ha il segmento esterno maggiore di una semicirconferenza viene svolta mediante la costruzione di una figura (ibid. 72-98). La lunula viene ricavata partendo da un trapezio avente tre lati uguali tra loro e la base maggiore tale che il quadrato sia il triplo del quadrato di uno dei lati minori³². Prima di riportare il metodo di dimostrazione a quello del primo caso, viene puntualizzata la condizione che il trapezio sia maggiore del semicerchio (ibid. 75 ss.). Sempre per costruzione e ricorrendo alle figure Ippocrate continua dimostrando i casi in cui l'arco esterno della lunula sia minore di un semicerchio, assumendo però l'ulteriore condizione che la figura che rende possibile la dimostrazione, un trapezio, sia minore della semicirconferenza (ibid. 99-160); ultimo caso è quello in cui sono da quadrare un cerchio e una lunula insieme (ibid. 161-206)³³.

Cambiano ha messo in luce come i passaggi eseguiti da Ippocrate nelle sue dimostrazioni siano in direzione opposta a quelli che avrebbe eseguito Euclide. Innanzitutto la proposizione assunta a principio e ricorrente in tutte e quattro le dimostrazioni, [A], non viene assunta come indimostrabile, bensì è una proposizione che Ippocrate dimostra mediante un'altra, [B]; ma anche quest'ultima deve essere stata dimostrata da Ippocrate, nonostante non sappiamo in che modo³⁴. Per Ippocrate il principio non è necessariamente indimostrabile, ma può invece essere una qualche proprietà dimostrata di un certo ente geometrico.

Soprattutto però il matematico procede per problemi, che prima pone e poi via via esamina e risolve. Euclide invece avrebbe cominciato dimostrando la proposizione più elementare [B], poi quella derivata [A], quindi avrebbe scelto come principio delle dimostrazioni seguenti [B] e non [A], ed infine avrebbe enunciato il problema (i diversi casi di quadratura) e avviatane la soluzione³⁵. Le dimostrazioni del secondo e terzo caso fanno anche pensare alla questione del diorismos, di cui si attribuisce l'invenzione all'accademico Leone (6 T1 e D1, Lasserre) e che invece qui viene messo in pratica: infatti, Ippocrate procede nelle dimostrazioni solo dopo aver dato le condizioni affinché il problema sia risolubile.

Di volta in volta si procede a risolvere il problema valutando sul momento quale principio usare, disegnando e cercando la soluzione nella figura stessa. La necessità logica delle quadrature, allora, "non fa intervenire esclusivamente parole e concetti. La dimostrazione si avvale non solamente della relazione logica tra le tappe intermedie ma anche dell'osservazione di una figura; la necessità della conclusione segue dall'osservazione della figura", sottolinea Netz³⁶. In tutte e quattro le dimostrazioni riportate da Eudemo, Ippocrate procede per costruzione basandosi su [A]. Siamo lontani dal sistema assiomatico-deduttivo euclideo.

Questa modalità di risoluzione è detta anche dagli antichi apagoge, intendendo però ora con questo termine l'analogo latino di reductio³⁷: un problema complesso viene risolto riducendolo ad un problema più semplice (Procl. Comm. a Eucl. 213,1ss: "la riduzione è un passaggio da un problema o teorema ad un altro, per mezzo del quale, sia esso già noto o sia stato risolto, anche quello proposto risulterà evidente).

Ippocrate spinse il suo metodo di riduzione fino a tentare di risolvere il problema della duplicazione del cubo mediante l'inserzione fra due grandezze di due medie proporzionali in proporzione continua a e 2a (D.-K. 42B4)³⁸: purtroppo non disponiamo (o Ippocrate non diede) di questa soluzione³⁹. Fu invece Archita a percorrere la via giusta⁴⁰, nuovamente procurando una soluzione pratica: infatti il segmento del cubo di volume pari al doppio del cubo di partenza si trova introducendo e muovendo tre superfici (un semicilindro, un cono retto e un toro⁴¹). Si tratta dunque di un diagramma mobile, un po' come quello che generava la quadratrice di Ippia⁴², la quale appartiene ugualmente a questo genere di geometria pratica. Proprio quel tipo di soluzioni pratiche che Platone rimprovera ai suoi allievi, come ricordato sopra.

Non riportiamo il testo di Eutocio che descrive la dimostrazione di Archita, ma daremo in breve la soluzione nel più rapido linguaggio della geometria analitica, restando però fedeli al senso della dimostrazione originale⁴³.

Siano  le lunghezze tra le quali trovare le medie. Poniamo su AC l'asse delle x; poniamo invece l'asse delle y su una normale ad AC per A nel piano ABC; l'asse delle z sarà invece una retta parallela a PM e passante per A. Si trova il punto P:

(1) 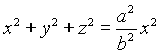 (cono)

(2)  (cilindro)

(3)  (toro).

Da (1) e (2) troviamo

(4) .

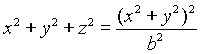Da (3) e (4)

(5) .

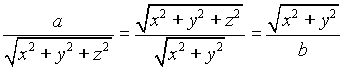Cioè

Da cui

. Ovvero, il cubo di lato AM sta al cubo di lato AB come AC sta ad AB. Ponendo il caso particolare  si ha , e avremo dunque raddoppiato il cubo⁴⁴.

Analogamente doveva procedere Antifonte sofista nella sua quadratura del cerchio: "Antifonte, descritto un cerchio, vi inscrisse uno qualsiasi dei poligoni tracciabili in esso" (D.-K. 87B13), e da qui continua. La dimostrazione venne giudicata non geometrica, poiché assume che "le grandezze sono divisibili all'infinito". In ogni caso, quello che ci interessa è che abbiamo sempre una dimostrazione che prende spunto dalle figure, come anche quella di Brisone⁴⁵.

E' appropriato menzionare adesso il Menone di Platone, nel quale Socrate vuol far dimostrare ad uno schiavo che il doppio di un quadrato si trova costruendo sulla sua diagonale un altro quadrato (82C-84A, 84D-85A). Durante l'esperimento Socrate fa ricorso passo dopo passo a delle figure che rendono evidenti i passaggi matematici da compiere⁴⁶. Lo schiavo è sconcertato dal constatare che raddoppiando il lato del quadrato la superficie si quadruplica (Men. 82B-84A). Vedendo la difficoltà nella quale sembra arenarsi, Socrate gli suggerisce: "Se non vuoi fare i calcoli, indicaci almeno da quale [lato si origina il quadrato doppio, N.d.a.]" (Men. 84A): gli propone cioè di aggirare l'ostacolo lavorando sulla figura, indicando quale sia concretamente il segmento risolutivo. Ma lo schiavo risponde espressamente di non saperlo. Così Socrate lo conduce a vedere che la soluzione sta nel costruire sulla diagonale del quadrato un ulteriore quadrato che avrà superficie doppia (Men. 84D-85B).

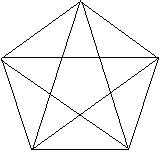
Trarremo un ultimo esempio da Ippaso, pitagorico del quale le fonti ci tramandano solo vaghe notizie sul fatto che ebbe a che fare sia con gli irrazionali sia con il dodecaedro, ossia con la superficie poliedrica regolare formata da dodici facce pentagonali (D.-K. 18A4): Von Fritz ha ipotizzato una reale connessione tra queste due possibili scoperte di Ippaso⁴⁷. Infatti, cercando il rapporto tra la diagonale e il lato nel pentagono regolare, Ippaso potrebbe aver osservato che le cinque diagonali vanno a formare un ulteriore pentagono. Provando a sottrarre reciprocamente lato a diagonale e diagonale a lato, sarebbe stato facile giungere alla conclusione che le due grandezze non hanno una misura comune, cioè non sono riducibili l'una all'altra, quindi sono incommensurabili. Nella dimostrazione matematica bisogna avvalersi del teorema per cui nel triangolo isoscele gli angoli (e i lati) alla base sono uguali per poter applicare il metodo della sottrazione reciproca, teorema che la tradizione attribuisce a Talete. Ma ancor prima bisogna osservare attentamente la figura: è la figura che suggerisce che la riproduzione dei pentagoni può andare avanti all'infinito, motivo per cui Von Fritz giudica questa dimostrazione chiaramente epagogica.
 
 

L'altra faccia della dimostrazione: rigore e astrazione

Già nel VI-V sec. dovevano circolare dimostrazioni di carattere diverso, nelle quali il ricorso alla pratica e all'evidenza era molto più debole se non addirittura assente. In fondo anche l'uso delle figure, abbiamo detto, significa procedere ad una prima riflessione, estrapolando dall'oggetto immediato qualcosa che inizialmente l'oggetto non ha. La tendenza all'astratto dei Greci ha però spinto questo fino alla smaterializzazione degli enti geometrici che diventano dunque enti immateriali e razionali sui quali poi potrà innestarsi l'ideale della forma dimostrativa.

In ambiente pitagorico doveva essersi prodotta una nota dimostrazione dell'irrazionalità della  (data da Aristotele in An. Pr. I 23 41a25 ss. e da uno scolio al libro X di Euclide⁴⁸), che, proprio per il rigore che la connota e per l'astrattezza che la rende facilmente formalizzabile, è giudicata apagogica da Von Fritz.

Sia dato il quadrato di lato l e diagonale d tale che, per assurdo, il rapporto d/l sia uguale a quello m/n di due numeri interi primi tra loro.
 
 

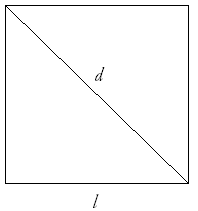
Per il teorema di Pitagora si ha: d² = l² + l², e da qui si trae che: (m/n)² = 2, ovvero m² = 2n². m sarebbe quindi necessariamente pari, essendo il suo quadrato divisibile per due, ed n sarebbe necessariamente dispari, essendo primo con m. Ma si potrà scrivere m = 2p, e sostituendo nell'identità m² = 2n², si otterrebbe: 4p² = 2n², da cui n² = 2p², e pure n dovrebbe quindi risultare pari. Giungiamo dunque all'assurdo che n è simultaneamente dispari e pari. Ciò significa che non esiste un numero razionale, un rapporto di interi, capace di esprimere il rapporto tra diagonale e lato, grandezze le quali pertanto risultano incommensurabili, ragion per cui si desume l'irrazionalità di .

Ma il matematico che più di tutti innestò la sensibilità e la possibilità per la matematica greca di essere astratta e formalizzata è senza dubbio Eudosso di Cnido. A lui si deve la precisazione e l'approfondimento del concetto di proporzione, concetto che in qualche modo già doveva essere usato - pensiamo alla testimonianza di Plutarco su Talete o alla media quadratica di Archita - ma che era usato in maniera grossolana e non cosciente. Un famoso scolio al V libro di Euclide⁴⁹ attribuisce ad Eudosso la formulazione dei contenuti di quello stesso libro, ovvero la teoria delle proporzioni: che tale teoria rappresentasse un salto di qualità nella matematica del tempo, quanto a rigore e profondità, lo stesso Euclide doveva averlo ben presente, se ritardò la sua introduzione al libro V e cercò di esporre il maggior numero di argomenti nei primi quattro libri⁵⁰.

Eudosso doveva aver raffinato il concetto di rapporto che già diffusamente si usava, anticipando in modo approssimativo quello di proporzione: si pensi al problema dell'altezza delle piramidi di Talete, o ai tentativi di quadratura del cerchio e di duplicazione del cubo. Ecco dunque la definizione di proporzione data da Euclide, corrispondente a V def. 5, e che appunto "non sembra sia opera personale di Euclide, ma viene attribuita concordemente al grande matematico Eudosso di Cnido"⁵¹:

V def. 5: "si dice che [quattro] grandezze sono nello stesso rapporto, una prima rispetto ad una seconda ed una terza rispetto a una quarta, quando risulti che equimultipli della prima e della terza [presi] secondo un multiplo qualsiasi, ed equimultipli della seconda e della quarta [presi pure] secondo un multiplo qualsiasi, sono gli uni degli altri, cioè ciascuno dei due primi del suo corrispondente fra i secondi, o tutti e due maggiori, o tutti e due uguali, o tutti e due minori, se considerati appunto nell'ordine rispettivo (= quando cioè presi equimultipli qualunque della prima grandezza e della terza ed equimultipli qualunque della seconda e della quarta, secondo che il multiplo della prima sia maggiore, uguale o minore del multiplo della seconda, l'equimultiplo della terza è corrispondentemente maggiore, uguale o minore dell'equimultiplo della quarta"⁵².

È noto che tale definizione è stata contestata da Galilei a causa della sua scarsa semplicità e che dunque non produce "nel lettore qualche concetto aggiustato alla natura di esse grandezze proporzionali"⁵³. Eppure proprio questa mancata semplicità probabilmente produce uno dei primi risultati di matematica astratta. Si è detto che il rapporto tra grandezze era un'idea già utilizzata, e troviamo quest'uso non solo nei primi matematici greci, ma addirittura potremmo risalire indietro fino alle matematiche dei popoli mesopotamici ed egizi⁵⁴. Euclide premette alla definizione di proposizione, allora, quella di parte, maggiore, minore, multiplo (V def. 1, 2), rapporto (V def. 3, 4⁵⁵). Allora si può dire finalmente dire (V def. 5) che due grandezze A e B sono nello stesso rapporto di due grandezze C e D quando, dati due interi (positivi) qualunque (cioè infiniti⁵⁶) m e n, si ha concordanza nei segni nelle espressioni:

mA < = > nB Û mC < = > nD. Basta che non si verifichi una sola concordanza di segni (dunque per un solo valore di m ed un solo valore di n) per concludere che i rapporti non sono uguali e dunque non sussiste proporzione.

Il segno di uguaglianza sussiste solo nel caso di grandezze commensurabili, in cui l'infinità dei valori di m ed n è un dato sovrabbondante. Se  ed , ad esempio, si avrebbe:  e , e dunque .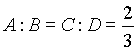

Per quelle incommensurabili bisogna procedere invece verificando infinite disuguaglianze. È un modo geniale per aggirare un ostacolo che generava un timore enorme nella speculazione greca: se m ed n possono assumere infiniti valori, ecco infatti che l'infinito entra in gioco. Ma Eudosso elabora un metodo per "imbrigliarlo"⁵⁷, "circuirlo", "circoscriverne" usi ed effetti; riesce a rendere rigoroso, astratto, formale un metodo che inevitabilmente si deve rifare all'infinito⁵⁸. È lo stesso meccanismo che gli permette di elaborare il metodo per esaustione, che per motivi di brevità non richiamiamo, data anche la sua notorietà⁵⁹.

Platone preferisce espressamente la matematica nelle sue vesti astratte. La severità del rimprovero - già ricordato - che il filosofo rivolge a coloro che fanno geometria "in modo ridicolo [...]" (527A-B) fa però contrasto con l'assiduo ricorso alle figure nel Menone. Inoltre la geometria viene considerata uno strumento per ricordare ciò che già si possiede (anamnesi⁶⁰), di contro a quanto viene dichiarato nella Repubblica dove la geometria è tra le discipline che restano come "sonnambuli nei confronti dell'essere, di modo che per esse è impossibile vederlo così com'è" (533B-C).

Cambiano sostiene che tra le due opere rappresenta uno spartiacque la svolta assiomatica di Eudosso e i dibattiti successivi. Platone, che poteva aver preso confidenza con il metodo di riduzione di Ippocrate, polemizza contro la decisione di fare della matematica un sistema formale basato su degli assiomi scelti per intuizione, propendendo per una scienza matematica procedente per ipotesi sempre perfettibili e migliorabili⁶¹.

Hösle reputa che sia erroneo cronologicamente collocare i lavori assiomatici di Eudosso prima della stesura della Repubblica. Piuttosto lo studioso reputa molto più probabile che siano stati i lavori di Leodamante di Taso, allievo di Platone, a mettere in discussione il maestro: infatti Leodamante, su invito di Platone⁶², sarebbe stato spinto ad applicare il metodo per ipotesi "fino in fondo", fino cioè agli assiomi⁶³. Se così fosse, sarebbero ancora più evidenti i motivi del cambio di prospettiva di Platone: ultimando il procedimento per ipotesi e trovando le "premesse prime" dei ragionamenti, diveniva ovvio che la geometria non poteva mostrare l'essere nella sua pienezza ma solo indicarlo approssimativamente. La questione allora si incentra sul senso ontologico che Platone poteva voler dare agli assiomi. Infatti per Platone ogni tipo di dimostrazione fa uso dello stesso metodo: l'anabasis. Cambiano però le assunzioni iniziali, cambia il punto dove fermarsi, e su ciò non avrebbe potuto non scontrarsi con quanti in Accademia sembravano voler decidere in maniera definitiva gli assiomi della matematica. Su questo Platone è molto duro, vedendo qui il motivo del sonnambulismo delle discipline come la geometria, l'astronomia e la musica ("finché almeno si servono di assiomi che lasciano indimostrati solo perché non sanno darne ragione", Repubblica 533C).

Nella logica di Platone c'è dunque spazio solo per la l'anabasis, e la vera scienza è la dialettica. Il procedimento è solo di "risalita" dalla realtà, realtà alla quale, una volta compresa come fonte di conoscenza, non si torna (a meno che non si voglia intendere come ritorno la successiva riflessione/contemplazione nella realtà che svela la divisione degli enti di natura "a discesa" da quanto prima guadagnato "risalendo" la catena delle Idee). Oggetto ultimo di intuizione sono le Idee, non certo la natura. È fortemente comprensibile, dunque, il perché nel Filebo (55C-57A) il filosofo distingua due aritmetiche: una materiale ed una formale. La prima, l'aritmetica "dei più", che altro non sarebbe che l'aritmetica applicata, si rivolge ai diversi oggetti materiali da misurare/contare ed in base alla diversa natura di questi oggetti fa uso di una diversa "unità" (ad esempio, l'unità con cui si contano due eserciti è diversa da quella con cui si contano due buoi); l'aritmetica formale, l'aritmetica "dei filosofi", fa uso di una sola unità.

La polemica si sarebbe allora potuta incentrare sul valore metodologico dell'intuizione: un conto è usare l'intuizione per definire gli assiomi a cui fermarsi; altro è usarla per continuare il processo di risalita fino alla contemplazione dell'Idea. È chiaro che si tratta di un modo diverso di concepire la matematica, e conseguentemente anche la natura e la realtà.

Probabilmente si può considerare conclusiva la VII Lettera: il filosofo fa consistere l'oggetto della conoscenza nel "vero essere" (342B): gli strumenti che noi adoperiamo (il nome, la definizione costituita di nomi e verbi e l'immagine costruita con riga e compasso - 342B-C) sono indispensabili, ma fallaci e decisamente inferiori all'intuizione intellettuale, che invece ci fa avvicinare all'essenza di ciò che vogliamo conoscere.

Intermezzo: le influenze del primo pensiero filosofico sul primo pensiero matematico

Prima di provare a trarre qualche conclusione sulla dimostrazione pre-euclidea, ci sembra importante fare un passo indietro e recuperare il contesto culturale nel quale operavano i primi pensatori di VI-V sec, poiché la tendenza all'astratto deve molto al pensiero non peculiarmente matematico. In quel tempo non si avevano una scienza matematica e una filosofia nettamente distinte, come d'altronde non si aveva l'astronomia, non si aveva la geografia, non si aveva la biologia. Eppure, si aveva una preziosissima abbondanza di conoscenze, più o meno particolari, diverse, prodotte ed elaborate in commistione: è la cosiddetta polymathia di VI-V sec.⁶⁴ I primi pensatori greci manifestarono abbondantemente la capacità di fissare, far circolare ed espandere molte conoscenze in ambiti diversi. Con particolare riguardo alla matematica, produssero saperi disparati, variegati, con i problemi pratici (D.-K. 11A1, 20, 21) e i teoremi (D.-K. 11A20) di Talete; con la scoperta degli irrazionali⁶⁵, l'algebra geometrica, il teorema di Pitagora⁶⁶ e molto altro; ci sono poi i problemi speciali, tra i quali abbiamo appena sfiorato quello della quadratura del cerchio, problemi che costituirono l'arena di alterchi e confronti tra Enopide, Ippocrate, Ippia, Antifonte, Brissone, Archita⁶⁷; infine troviamo Democrito, che è noto principalmente per aver trovato il volume della piramide e del cono⁶⁸ e che scrisse molti trattati tra cui uno Sulla tangente e Sulla costruzione prospettica dei raggi (Diog. Laert. IX 47-48). E molto ancora.

L'interesse dei Presocratici fu eterogeneo e a tutto tondo e produsse una quantità smisurata sia di logoi che di doxai, che troppo spesso vengono dimenticati a vantaggio di sezioni scelte di sapere. Anche in ambiti che sembrano lontani dalla scienza e che per questo potrebbero sembrare inutili ai nostri fini, gli antichi Greci misero in luce un modo nuovo di guardare alla realtà⁶⁹.

Nonostante rimanga un sapere variegato e composito, la polymathia attesta espressamente che c'era il desiderio di spiegare e capire la complessità della realtà, introducendo nella storia dell'umanità un modo nuovo di guardare agli eventi naturali, che non sono più il veicolo dell'ira degli dei bensì fenomeni da esaminare e ricondurre a cause naturali⁷⁰: si pensi alla famosa critica di Senofane all'antropomorfismo degli dei⁷¹. All'interno di questo panorama si pongono anche domande curiose, incalzanti, apparentemente paradossali o di risoluzione impossibile: Talete vuole misurare l'ampiezza angolare del sole e dopo lui si inizia a cercare l'arche, Eraclito osservando un fiume sentenzia che non vi ci si può bagnare due volte, i Pitagorici si interrogano sull'armonia dei cieli. Il genio greco si spinge fino a domande apparentemente inutili, che non soddisfano nell'immediato ad una qualche esigenza pratica: è l'episteme per l'episteme.

A fianco a questo o forse in conseguenza, si cominciano a cercare teorie generali: "non voglio sapere la causa di questo fenomeno, ma la causa di tutti i fenomeni" (la dottrina del principio); "come respirano tutti gli animali" (Empedocle); "come costruire un calendario in cui dar conto dei cicli solari e di quelli lunari" (la questione del "grande anno"⁷²). Ciò avviene ancor più evidentemente in ambito matematico: "non mi interessa l'altezza di quella precisa piramide: voglio poter calcolare l'altezza di tutte le piramidi" (Talete); "non mi interessa sapere il valore approssimativo dell'area della superficie di questo cerchio: voglio sapere come quadrare tutti i cerchi" (i problemi speciali); "non mi interessa sapere come rappresentarmi una certa costruzione solida: voglio sapere quali sono i solidi perfetti" (Pitagorici). Il carattere universale dei problemi posti è senza dubbio una novità nel panorama della cultura del tempo e non credo sia avventato dire che rappresenti una "scoperta" che qualificò il pensiero occidentale. Prendendo le mosse dall'osservazione della realtà, il genio greco rese quella stessa realtà ancor più sorprendente, cercando di comprenderne in profondità la struttura, senza evitare di ricorrere ad ardue astrazioni.

Nella conoscenza matematica ciò è quanto mai evidente: le prime riflessioni vertono su problemi concreti ma subito si rivolgono a questioni dotate di una certa universalità e apparente "inutilità". A ciò si deve aggiungere una preponderante degli inizi della matematica, consistente nel suo legame con problemi di tipo geometrico. Questo legame potrebbe motivarsi nel fatto che la geometria è la scienza che più nell'immediato traduce la realtà che ci circonda: guardiamo l'orizzonte, il sole o la luna e vediamo un cerchio; tracciamo i confini di un terreno e riproduciamo un rettangolo; costruiamo un monumento e riproduciamo un cubo; e così via. Non sono di certo pochi gli esempi che rendono evidente l'etimologia del termine stesso "geo-metria" e che in parte giustificano alcune riduzioni della prima matematica greca ad agrimensura⁷³. È cioè quanto di più naturale potesse avvenire e rimanda a tutto ciò che si è detto sull'uso dell'intuizione e dell'evidenza nelle prime dimostrazioni.

Contrasta con questa lettura Netz che, adducendo a prova le dimostrazioni di Ippocrate e l'aferesi, sostiene che in questo periodo la matematica non aveva ancora troppo stretto le sue sorti con la geometria e che il nostro punto di vista è alterato da quello dei matematici del IV secolo, che erano interessati a dimostrazioni e figure e dunque non presero in considerazione risultati di natura aritmetica⁷⁴.

Se ha senso sostenere che non si possa parlare di "matematica greca" come una disciplina autonoma fino al IV secolo, poiché l'approccio al sapere era del tipo della polymathia, torniamo a dire che il rischio è di identificare la matematica greca con quella specificatamente aristotelico-euclidea, mentre invece si è visto che non era l'unica matematica, che pur fu quella ad avere nei secoli maggior successo.

Sta di fatto che ci vuole del tempo affinché le diverse discipline si differenzino e si possa dunque avere una "scienza matematica" tout court. Cosa ne permise l'emergere se i suoi risultati erano accumulati (forse dispersi) nel sapere della polymathia o come riuscì la matematica a configurarsi come disciplina autonoma, mantenendo insieme l'aspetto pratico e quella forte tendenza all'astratto che innegabilmente la rese "greca" sono interrogativi ai quali è importante rispondere. Per provare a comprendere meglio questa spinta al sapere "inutile ed universale", questo innesto dell'astratto sul reale e avere luce sulle origini dell'idea di dimostrazione deduttiva ci sembra che non si possa prescindere da Parmenide e l'Eleatismo.

La prassi è di citare tra gli Eleati solo Parmenide e Zenone nelle storie della matematica o della logica⁷⁵ per l'invenzione del principio di non contraddizione o della prova per assurdo. Per via di quest'ultima Szabó attribuisce all'Eleatismo un posto d'onore nel processo di costituzione sistematica della matematica, per spiegare il passaggio da una matematica di carattere empirico - come poteva essere non solo quella orientale ma anche quella ionica - ad una matematica astratta⁷⁶. In effetti che tale dimostrazione ebbe una risonanza di non poco conto nella storia del pensiero è confermato anche dal fatto che venne ampiamente utilizzata negli Elementi.

La centralità che Szabó attribuisce all'Eleatismo nella nascita della matematica potrebbe far sorgere diversi dubbi: ad esempio come mai i matematici greci non aderirono alla filosofia eleatica⁷⁷. Ci sono anche ulteriori osservazioni: primo, non tutta la matematica precedente a Parmenide era così "materiale" come sembra passare in questa interpretazione - basta interrogarsi sul senso delle generalizzazioni matematiche di Talete; secondo, non tutta la matematica successiva a Parmenide sarà soltanto astratta - basti pensare al filone applicativo che poi riemergerà con Archimede fino ad Erone.

Ciò a cui Parmenide e l'Eleatismo diedero un contributo considerevole è senz'altro la stessa idea di "dimostrazione rigorosa": ed è proprio l'idea che tra tutte le discipline e le scienze contraddistingue la matematica. Con l'Eleatismo il salto di qualità, rispetto alla polymathia nella quale anche i Milesi sembravano disperdersi, è senza dubbio sorprendente.

Va notato con forza che indubbiamente Parmenide propone un nuovo modo di "dimostrare" e propone una maniera nuova di "astrarre"⁷⁸. Per quanto riguarda l'emergere del desiderio di controllare il sapere e renderlo incontestabile, sembra infatti che l'apporto di Parmenide vada oltre la scoperta del principio di non contraddizione. Questo principio - o meta-regola - è stato infatti la pietra angolare sulla quale il Poema sviluppa un sistema comunicativo veramente significante ed efficace. Con Parmenide il sapere viene esibito in forma "non contraddicibile": il giovane filosofo ascolta la dea con attenzione, e la dea parla svelando la forza delle sue conoscenze, indiscutibili, certe. Su cosa si basa la forza persuasiva del discorso della dea? Non certo sulla trascendenza del sapere di cui la dea è depositaria, bensì sull'evidenza del ragionamento: mediante un esame dettagliato del Poema e della struttura delle argomentazioni della dea, Rossetti ha messo in evidenza che nel Poema di Parmenide:

"…la sua dea costruisce veri e propri itinerari argomentativi, sa cosa sono le premesse, le questioni preliminari, gli stessi errori di prospettiva, si dedica a sgomberare il campo da simili intralci e sa di farlo; la sua dea sa fornire indizi e prove, e sa svolgere corollari rendendosi conto della specificità di queste componenti; la sua dea sa individuare il punto cruciale e il passaggio dell'argomentazione e non manca di segnalarlo"⁷⁹.

Inutile dire quanto tutto ciò sembri anticipare le regole dell'assiomatica: porre premesse, svolgere l'argomento in demostrandum e conseguire la certezza del provato. Parmenide mira ad esibire un ragionamento indiscutibile, incontrovertibile perché basato sugli strumenti della ragione tanto che Rossetti ne definisce l'atteggiamento come di un antisocratico "so di sapere"⁸⁰.

Così le distanze verso un sapere ben costituito, ben fatto, giustificato nelle sue parti sembrano raccorciarsi rapidamente. Il salto di qualità è ragguardevole: se la polymathia veicolava un sapere molteplice, curioso e spesso geniale, ciò che in essa poteva timidamente affiorare come un ideale da raggiungere - ovvero l'astrattezza e l'universalità di certe conoscenze, la versatilità e l'applicabilità a molti casi di uno stesso ragionamento - con Parmenide diviene quasi una richiesta preliminare, una regola alla quale la conoscenza deve sottostare. La forza di un sapere va a risiedere nella capacità di dimostrarlo.

Verso dove si direziona il discorso parmenideo? Da dove trae il suo rigore e la sua forza? Dall'essere. La strada proposta dalla dea, la strada dell'essere, è paradossalmente l'unica via per sapere tutto "sia della verità rotonda il sapere incrollabile sia ciò che sembra agli uomini, privo di vera certezza. Saprai tuttavia anche questo, perché le parvenze dovevano plausibilmente stare in un tutto, pur tutte restando" (fr. 1 vv. 26-30). Nonostante già Platone dovesse ritenere superflua la parte del Poema di Parmenide dedicata alla filosofia della natura, e nonostante studiosi come Zeller o Gomperz vi abbiano analogamente sorvolato, l'abbondanza dei versi ad essa dedicati ed affermazioni come quella appena riportata dovrebbero far riflettere: segue questa direzione Cerri, che riabilita il Parmenide erede delle dottrine ioniche come perfettamente coniugabile con il Parmenide della dea. "Il discorso scientifico cerca di seguire la via dell'essere, elaborando i dati dell'esperienza fin dove gli è possibile, unificando tutto l'unificabile"⁸¹.

Con Parmenide si inizia ad argomentare mostrando la ratio che accomuna tutti i fenomeni e ne svela la verità: l'essere. Tutti i fenomeni prima di essere fenomeni semplicemente sono. La Curd sembra spingere questo discorso al punto da affermare che "il suo [di Parmenide, n.d.a] "è" è un "è" predicazionale di tipo particolarmente forte piuttosto che un "è" esistenziale". Come dire: se anche Parmenide fu monista, non lo fu in senso numerico (ovvero nel senso che "esiste una cosa sola"), piuttosto in senso predicazionale. Il monismo predicazionale è "l'affermazione che ogni cosa esistente può essere soltanto una cosa; e deve esserlo in un senso particolarmente forte"⁸².

Ma anche senza scendere nella questione se l'essere di Parmenide vada preso secondo una valenza più epistemologica o più ontologica, va rilevato che, in ogni caso, è lo stesso procedere argomentativo che deve rispecchiare la logica intrinseca alle cose: muovendo da premesse, tramite passaggi logici si costruisce un'argomentazione che rispecchia la realtà profonda delle cose e dunque è essa stessa essere. Il discorso è vero qualora riflette la verità della realtà. Emerge la valenza fondativa del discorso scientifico: il discorso ben fatto e ben condotto diviene veicolo della struttura profonda della realtà. Consegue che saper dimostrare diventa essenziale per colui che pretende di sapere: paradossalmente è svolgendo la sua capacità "dimostrativa" che Socrate conduce l'altro all'ammissione di non-sapere.

Più noti i paradossi di Zenone, con i quali si afferma sempre più l'ideale della verità conquistato mediante la logicità del ragionamento: di fronte al paradosso la ragione si trova a prima detta schiacciata, e solo con una argomentazione altrettanto logica si può pretendere di affermare il contenuto opposto. Diventa, dunque, importantissimo imparare l'uso degli strumenti logici e dialettici per argomentare bene e far vincere le proprie opinioni, anche se indubbiamente in Zenone è del tutto assente l'idea di sistema assiomatico-deduttivo, poiché le sue confutazioni sono rivolte ad una singola proposizione, e non certo ad un sistema di proposizioni⁸³. Ma se ancora in Zenone l'uso della dimostrazione non è circoscritto a una scienza specifica ma - potremmo dire - è trasversale al sapere in generale, con Melisso questo uso si cala in un ambito ben più specifico, tanto che sembra inventarsi una disciplina a parte con un suo linguaggio proprio: la metafisica⁸⁴.

Quest'ultimo non viene mai citato nelle storie del pensiero matematico né nei tentativi di ricostruzione storica dell'idea di dimostrazione⁸⁵. Invece, spingendo all'estremo il pensiero di Parmenide e sfociando in un assoluto monismo ontologico, Melisso ripropone i suoi argomenti⁸⁶ secondo un rigore che sorprende per il tempo, addirittura inventando un nuovo linguaggio, nuovo perché scrive in prosa e scrive di ontologia. I fr. 7 e 8⁸⁷ sorprendentemente sono una successioni di asserzioni condizionali con l'antecedente al congiuntivo (controfattuali), che ipotizzano ciò che sarebbe accaduto (o non sarebbe accaduto) nel caso del verificarsi (o non verificarsi) di determinate condizioni: se fosse soggetto… non potrebbe essere, se fosse alterato… non sarebbe perito, e così via, via a dimostrare una per una le tesi volute⁸⁸.

Conclusioni: l'emergere della ratio mathematica e l'idea di dimostrazione

Giungiamo dunque ad un punto cruciale per il nostro discorso. La polymathia del VI-V secolo aveva raccolto una quantità smisurata di conoscenze in tanti e diversi abiti di sapere. Per quanto riguarda la matematica erano stati ottenuti risultati di rilievo sia nelle ricerche di ispirazione puramente aritmetica e geometrica come anche lavorando nell'ambito dell'astronomia e della tecnica. Si trattava di conoscenze scollegate, spesso estremamente diverse, fortemente ancorate all'esperienza e alla visione diretta.

D'altro canto l'eleatismo aveva innestato la tendenza a strutturare le conoscenze esibendone la ratio caratteristica e a dimostrare la capacità e la certezza del proprio ragionamento. L'idea di dimostrazione diventa sempre più centrale nel pensiero filosofico greco. Ora, era chiaro che la ratio individuata da Parmenide (l'essere) era troppo vasta e soprattutto non permetteva di sistemare adeguatamente in un unico quadro organico le tante scoperte fatte.

Il materiale matematico disponibile aveva questo pregio: poteva cioè esibire in modo abbastanza immediato una ratio particolare. I dati dell'aritmetica e soprattutto della geometria⁸⁹ presentavano una comunanza quasi naturale, una specificità che di certo li distingueva dai risultati della medicina, della storiografia, della meteorologia. Da qui immaginare di sistematizzarli non doveva essere troppo assurdo. È cioè realistico credere che gli ingegni greci cominciarono a lavorare, discutere, ragionare per mettere insieme tutto ciò di cui disponevano.

C'è di più. Questo materiale sembrava particolarmente adatto ad essere "dimostrato", ad essere esposto o provato con dimostrazioni. La matematica era in grado di individuare una ratio semplice, immediata. E soprattutto le dimostrazioni che "giravano intorno" alla ratio delle cose matematiche "funzionavano": questo non poteva che suscitare fascino.

Ma dovette suscitare anche aspre polemiche. L'ideale di un sapere universale, rigoroso e quindi astratto andava in contrasto con un modo di procedere che continuamente ricorreva alle immagini e alle soluzioni pratiche. D'altra parte si è visto che anche nell'ambito dell'Accademia doveva esistere un dibattito così animato sul valore e sull'organizzazione della matematica da far pensare che già si era molto lavorato e le opinioni che si erano andate formando tra VI e IV secolo dovevano essere già molto varie. Erano attivi nell'Accademia Leodamante di Taso, considerato inventore del metodo per ipotesi (2 D1-2, Lasserre); Teeteto, considerato ideatore di molti dei contenuti del libro XIII di Euclide (3 D32-41, 42f, Lasserre), libro che procede in gran parte per problemi (prop. 12-18). Ma molti geometri dell'Accademia dovevano andare in direzione diversa: Teudio cercava di generalizzare proposizioni particolari, probabilmente risalenti a Ippocrate (14 F2, Lasserre); Anfinomo cercava di distinguere i teoremi dai problemi (18 D2, Lasserre), e a loro volta i problemi in problemi a prescrizione, problemi intermedi e problemi senza prescrizione (18 D3, Lasserre), fino a chiedersi anche come poter invertire termini generali e particolari (18 D4, Lasserre)⁹⁰; anche Filippo d'Oponte studia come distinguere teoremi e problemi (20 F20, Lasserre).

In certi casi la contrapposizione doveva anche essere netta: si pensi alla diversa concezione delle proposizioni della geometria, per cui secondo Anfinomo sono teoremi e dunque vertono su cose eterne (18 D2, Lasserre), mentre per Menecmo sono problemi e dunque sempre rivisitabili (12 D5, Lasserre). L'attività degli Accademici doveva in ogni caso incuriosire e stimolare, probabilmente lo stesso Aristotele, che si trovava finalmente a confrontarsi con un concetto di scienza diverso rispetto a quella platonico⁹¹.

La dimensione empirica di un certo sapere matematico non fu abbandonata velocemente o improvvisamente⁹²; tutt'altro, visto il riemergere dell'interesse per le applicazioni pratiche dimostrato, come già detto, in autori più tardi quali Archimede o Erone.

Le vesti astratte del ragionamento scientifico vengono dunque tessute lentamente e progressivamente, sopra dimostrazioni di genere diverso nelle quali il ricorso all'evidenza intuitiva e alle figure era decisivo. Le due radici - epagogica ed apagogica, per dirla con Von Fritz - della dimostrazione a lungo si intrecceranno, tenendo insieme elementi deduttivi ed elementi induttivi e ricorrendo contemporaneamente sia a passaggi astratti che a figure appositamente costruite.

Vogliamo concludere questa tentata ricostruzione dell'idea euclidea di "dimostrazione" tornando ad Aristotele, dal quale siamo partiti e sul quale si proverà a tracciare qualche riflessione e fare qualche ipotesi senza alcuna pretesa di conclusività. In diverse occasioni è stata messo in luce la stretta corrispondenza tra la struttura della scienza così come pensata e delineata dallo Stagirita negli Analitici Secondi e gli Elementi di Euclide⁹³. Se Aristotele distingue definizioni, assiomi, nozioni comuni, teoremi, problemi, Euclide anche distingue postulati, termini, nozioni comuni, dimostrazioni, problemi e così via⁹⁴.

Inoltre Aristotele provvede a teorizzare ampiamente la necessità per la scienza di svolgere deduzioni rigorose e svolgerle correttamente solo all'interno di un intero sistema di proposizioni tra le quali alcune di esse almeno parzialmente irrevocabili. La stessa sillogistica di Aristotele mostra la verità di questo presupposto, poiché le varie tesi del sistema danno per validi alcuni assiomi⁹⁵. Solo il riferimento ad un sistema rende possibile anche la stessa confutazione di tesi sbagliate: se così non fosse, Zenone avrebbe avuto ragione, mentre invece Aristotele lo critica muovendo dal suo proprio sistema⁹⁶.

In secondo luogo, il metodo analitico non può procedere da solo ma ha comunque bisogno di fermarsi ad un punto e "essere subordinato" a quello sintetico, per permettere alla conoscenza di progredire deducendo mediante l'inventio medii⁹⁷. Per questo il sistema di Aristotele potrebbe essere definito analitico-deduttivo: diverso, dunque, dal sistema ipotetico-deduttivo così come oggi potremmo pensarlo, poiché la ricerca degli assiomi non va indefinitamente a ritroso ma può tornare alla realtà. Questo ideale di dialogo con la realtà costituisce il cuore della stessa scienza. "Uno sa ciò che impara" (An. Sec. I 1 5-7): è questo il movente della sua critica alla dottrina dell'anamnesi, la quale delega ad un misterioso passato - su cui in fin dei conti non si ha alcun potere - la ragione del mio conoscere (cf. An. Post. I 71b5-8)⁹⁸.

Affermazioni di Aristotele come: "chi è esperto in geometria non trae tuttavia alcuna conclusione per il fatto che tale linea concreta sia la linea di cui egli ha parlato, ma si deve piuttosto dire che le sue conclusioni sono chiarite da questi oggetti concreti" (An. Sec. 10 77a1-3) vengono illuminate da un portato teoretico di sfondo che non abbandona la conoscenza, nata mediante l'esercizio pratico ad un ruolo non ben delineato. Il geometra non può fare a meno di ricorrere all'astrazione (se infatti disegna una linea che deve essere lunga un piede, non è necessario che sia lunga un piede, né che sia precisamente retta) ma al contempo non può privarsi di rimandare al concreto (le conclusioni del suo ragionamento devono essere poi confermate e rese chiare dalla realtà). Analogamente non si può rinunciare alla visione concreta delle cose in geometria: "…se, infatti, fosse già tracciata la parallela ad un lato del triangolo, alla semplice visione della figura la cosa risulterebbe immediatamente evidente" (Metaph. Q 9 1051a24-27). La vista può pretendere di decidere l'autenticità di una affermazione, come risulta ancor più chiaramente in Metaph. Q 9 1051a21-33: "anche i teoremi di geometria si dimostrano per mezzo dell'atto, infatti si dimostrano operando delle divisioni nelle figure (…)".

Ciò non significa che Aristotele rimandi tutto alla vista e all'evidenza nella costituzione della sua scienza, come già emerge nella citazione appena letta. "I teoremi della geometria si dimostrano all'atto": è mediante l'atto che viene mostrata la validità di un teorema, come mediante l'atto si possono trovare i primi principi dai quali discende la deduzione dimostrativa. Volendo correggere Platone, infatti, lo Stagirita intende rifiutare il regresso all'infinito nella ricerca degli assiomi, nella consapevolezza che ad ogni modo questa ricerca è un continuo e perfettibile viaggio, nel quale l'intuizione ha un ruolo significativo insieme al raziocinio. È il nous che intuisce i principi della scienza e fa ciò che la ragione deduttiva non è in grado di fare⁹⁹.

Ma il nous aristotelico che viene coinvolto nella costituzione del sistema assiomatico della scienza (discusso in particolare in An. Pr. II 23, An. Sec. I 23, II 19) non è intuizione "psicologica", non una facoltà innata, bensì una exis, un habitus ottenuto mano a mano che acquisisco e produco scienza¹⁰⁰. Questo fa sì che gli axiomata aristotelici ottenuti mediante l'intuizione non sono fondati su di un'evidenza di tipo cartesiano, come Cellucci sembra intendere¹⁰¹; o per lo meno, non tutti. Se infatti possono godere di evidenza visiva certi principi primi della geometria¹⁰², i tre principi di identità, non contraddizione e terzo escluso godono di un altro tipo di evidenza, prodotta mentre lo stesso intelletto si pone in atto¹⁰³. I tre principi, così, permettono la conoscenza scientifica ma anche lo stesso umano pensare; da lì ogni scienza poi cerca i suoi propri principi, ma nella consapevolezza che ci potrebbero essere altre possibilità¹⁰⁴. Per dimostrare questo delicato passaggio occorrerebbe chiarire il significato dell'induzione in Aristotele, cosa che per ragioni di spazio non è conveniente svolgere ora¹⁰⁵.

La complessità di questo processo di costituzione degli assiomi e del ruolo dell'evidenza che - torniamo a ripetere - andrebbe ulteriormente indagato ed approfondito, ovviamente ad Euclide non interessa. D'altronde Euclide è un matematico, e il suo compito storico è stato quello di mettere ordine in maniera pregevole a tutte quelle conoscenze particolari che nel corso di più di due secoli erano state accumulate.

Per secoli l'impianto euclideo resterà modello di scienza matematica deduttiva¹⁰⁶, e già presso i Greci dovette certo suscitare estrema ammirazione, poiché finalmente sembrava concretizzarsi l'ideale di un sapere apparentemente incontrovertibile.
 
 

¹ Á. Szabó, Les débuts des mathématiques grecques, Libraire Philosophique J. Vrin, Paris 1977, p. 200: "que nous n'ayons découvert aucune trace d'une mathématique systématico-déductive dans les civilisations préhelléniques ne saurait être dû à des lacunes dans nos connaissances".

² K. Von Fritz, Le origini della scienza in Grecia, Il Mulino, Bologna 1988, p. 212.

³ Come si legge anche in H. G. Liddell - R. Scott, A Greek English Lexicon, Clarendon Press, Oxford 19969, p. 174 il primo significato di apagoge è proprio quello di "leading away" e "separation". Come ultimo significato il Liddell-Scott riporta anche quello logico di "shifting of the basis of argument" e di reductio, significato che richiameremo in seguito.

⁴ Cf. C. Cellucci, Filosofia e matematica, Laterza, Roma-Bari 2003, p. 256.

⁵ Ibid., pp. 261-262.

⁶ Cf. R. Netz, The Shaping of Deduction in Greek Mathematics. A study in cognitive history, Cambridge University Press, New York 2003, pp. 26-35.

⁷ Ibid., pp. 17-19.

⁸ Utilizzo la raccolta di F. Lasserre (edition, traduction et commentaire), De Léodamas de Thasos à Philippe d'Oponte. Témoignages et fragments, Bibliopolis, Napoli 1987.

⁹ Netz è fermo nello stabilire l'origine di una "matematica greca" vera e propria addirittura in Platone e Aristotele. R. Netz, La matematica nel V secolo in Storia della Scienza. Vol. I La scienza greco-romana, Enciclopedia Italiana Treccani, Roma 2001, pp. 754-763, p. 763.

¹⁰ G. R. Giardina, Erone di Alessandria. Le radici filosofico-matematiche della tecnologia applicata. Definitiones, traduzione e commento, Symbolon - Università di Catania, Catania 2003, p. 96. La studiosa catanese interpreta la matematica greca come luogo di compresenza tra due tradizioni: quella pitagorico-platonica e quella aristotelica-euclidea. Entrambe le tradizioni producono "matematica", sebbene di carattere diverso: ma non possiamo favorirne una per dimenticare l'altra, se vogliamo avere una visione completa e rispettosa della matematica greca. Cf. ibid. pp. 96-102.

¹¹ Nonostante il numero pitagorico abbia i caratteri dell'arche, non è detto che questo arche non abbia radici in un forte riferimento all'orizzonte esperienziale. Ciò sarebbe in continuità con una eventuale interpretazione dell'arche di Talete, che ho proposto in F. Marcacci, Il riduttivismo di Talete in "Aquinas" 3 2004. Cf. P. H. Michel, De Pythagore a Euclide. Contribution a l'histoire des mathématiques préeuclidiennes, Société d'Édition "Les Belles Lettres", Paris 1950, pp. 295-312.

¹² Cat. XIV 15a29-32: "il quadrato ad esempio risulta bensì accresciuto, una volta che attorno ad esso sia stato applicato lo gnomone, ma rispetto alla qualità non risulta per nulla modificato".

¹³ Elem. II def. 2: "si chiami gnomone, in ogni parallelogramma, uno qualsiasi dei parallelogrammi posti intorno ad una sua diagonale insieme coi due complementi (= la somma di uno qualsiasi dei parallelogrammi posti intorno ad una sua diagonale e dei due complementi).

¹⁴ Cf. T. L. Heath, A history of Greek Mathematics. Vol. I. From Thales to Euclid, Dover Publications, New York 1981 (rist. anast. dell'ed. Clarendon Press, Oxford 1921), pp. 78-79.

¹⁵ Per i frammenti e le testimonianze sui Presocratici si fa riferimento alla raccolta I Presocratici. testimonianze e frammenti. Vol. I e II, a c. di G. Giannantoni, Laterza, Roma-Bari 2002 (tr. it. di A.A.V.V. di H. Diels - W. Kranz, Die Fragmente der Vorsokratiker. Griechischen und Deutsch, Berlin 196612; sigla D.-K.).

¹⁶ Cf. H. Hankel, Zur Geschichte der Mathematik in Alterthum und Mittelalter, 1874 cit. in G. Loria, Le scienze esatte nell'antica Grecia, Cisalpino-Goliardica, Milano 1987 (rist. anast. dell'ed. Hoepli, Milano 1914), p. 17.

¹⁷ Heath, Gr. Math., p. 131.

¹⁸ A. Frajese, Talete di Mileto e le origini della geometria greca, BUMI 1941, pp. 7-8.

¹⁹ P. Tannery, La géometrie grecque, comment son histoire nous est parvenue et ce que nous en savons. Essai critique. Histoire générale de la géométrie élémentaire, Olms, Hildesheim 1988 (rist. anast. dell'ed. Gauthier-Villars, Paris 1887), p. 90.

²⁰ Cit. in Loria, Le scienze esatte..., p. 17.

²¹ Heath, Gr. Math., p. 131.

²² Russo semplicemente ammette questo primo senso del termine apodeiknumi come "mostrare", "esporre". L. Russo, La rivoluzione dimenticata. Il pensiero scientifico greco e la scienza moderna, Feltrinelli, Milano 20012.

²³ Moritz Cantor, Geschichte der Mathemathik, cit. in Heath, Gr. Mat., p. 131.

²⁴ Se ne parlerà più avanti a proposito di Eudosso, § L'altra faccia della dimostrazione... .

²⁵ Conoscenza di certo posseduta già dagli Egiziani in quanto necessaria per la progettazione delle piramidi. Addirittura essi erano in grado di calcolare il volume di un tronco di piramide. Cf. C. B. Boyer, Storia della matematica, ISEDI, Milano 1976, pp. 23-24.

²⁶ L'ipotesi dell'impiego di strumenti da parte di Talete è esplicitamente formulata e adottata da Bretschneider per risolvere la questione del calcolo della distanza delle navi dalla riva. Cf. C. A. Bretschneider, Die Geometrie und die geometer vor Euclides. Ein historisches versuch, Sändig Reprint, Vaduz 1988 (Ripr. facs. dell'ed. Leipzig, Teubner 1870). Il tipo di strumento descritto da Bretschneider, cioè un cilindro cavo con un filo a piombo, è in realtà identico ad uno strumento utilizzato dagli egiziani per le misurazioni di estensioni lineari. Non sappiamo se lo studioso tedesco ne fosse a conoscenza, ma la coincidenza del dato conferma la fattibilità dell'impiego di strumenti. Cf. O. A. W. Dilke, Mathematics and Measurement, British Museum Publications Ltd, London 1987, pp. 7-8.

²⁷ È discusso se Ippocrate avesse avuto maestri pitagorici o se invece fosse stato contaminato dalle dottrine pitagoriche nel corso del suo lungo soggiorno ad Atene; in ogni caso è sicuro che ebbe stretti contatti con la Scuola; cf. M. Timpanaro Cardini (a c. di), Pitagorici. Testimonianze e frammenti fasc. II, La Nuova Italia Editrice, Firenze 1962, pp. 28-31. Sul pitagorismo di Ippocrate cf. in particolare D.-K. 42A2, 5.

²⁸ La lunula (= menisco o anche segmento di cerchio) è quella parte di piano racchiusa tra due archi di cerchio, di raggio diverso ma con i medesimi estremi. Questa figura sembra essere un'invenzione di Ippocrate, escogitata proprio per il problema della quadratura. Euclide infatti riporta la definizione di lunula come segmento di cerchio, cioè quella figura compresa tra un arco di cerchio e la corda sottesa (III def. 6). Solo nel 1903 si è pervenuti al calcolo del numero (finito) delle lunule quadrabili (cf. A. Piccato, Dizionario dei termini matematici, Rizzoli, Milano 1987, p. 264).

²⁹ Metone e Pistetero ne Gli uccelli (nell'edizione di Aristofane, Tutte le commedie, a c. di G. Padano - ed. integrali, Newton, Roma 1991, p. 244).

³⁰ Cf. Timpanaro Cardini, Pitagorici, pp. 46-47.

³¹ Euclide non conserva nei suoi Elementi questa proposizione, che probabilmente era contenuta negli Elementi di Ippocrate, mentre invece mantiene quella sul rapporto tra i cerchi e i quadrati dei diametri (XII.2).

³² Simplicio fornisce una dimostrazione erronea per la costruzione di un trapezio siffatto.

³³ Alessandro di Afrodisia ci riporta anche altre due dimostrazioni che giudica ippocratee. Ma queste contengono delle contraddizioni così evidenti che sembra difficili sia veramente del geometra di Chio; piuttosto, si può pensare che Aristotele si riferisse a questi errori quando giudicasse erronee le dimostrazioni di Ippocrate (D.-K. 42A3), pur giudicandolo altrove valente geometra (D.-K. 42A2). Cf. Heath, Gr. Mat., pp. 184-185.

³⁴ Heath presuppone che in qualche modo Ippocrate anticipò il metodo di esaustione, poiché anche Euclide dimostra questa proposizione mediante esaustione, appoggiando al principio di Archimede (XII 2). Cf. Heath, Gr. Math., p. 202.

³⁵ G. Cambiano, Il metodo ipotetico e le origini della sistemazione euclidea della geometria, Rivista di Filosofia, 1967, pp. 129-130.

³⁶ Netz, La mat. nel V sec., p.760.

³⁷ Non quindi apagoge nel senso iniziale dato da Von Fritz, che si richiama all'etimologia del termine.

³⁸ Cf. Timpanaro Cardini, Pitagorici, pp. 60-63.

³⁹ Sia a lo spigolo del cubo. Si tratta di trovare due segmenti x e t tali che a : x = x : y = y : 2a.

⁴⁰ Cf. Timpanaro Cardini, Pitagorici, pp. 296-307.

⁴¹ Di diametro interno pari a zero, cioè tale che il suo asse di rotazione sia tangente al cerchio. Cf. P. A. Giustini, Da Euclide ad Hilbert. Dal miracolo greco alle geometrie non euclidee, Bulzoni Editore, Roma 1974, p. 50.

⁴² Si tratta di una curva che si origina mediante la combinazione di un moto circolare e un moto curvilineo. La curva può essere utilizzata sia per quadrare il cerchio sia per risolvere l'altro "problema speciale" della trisezione dell'angolo. Cf. Heath, Gr. Math., pp. 226-230.

⁴³ La dimostrazione analitica è trascritta da Giustini, Da Euc. ad Hilb., pp. 51-52.

⁴⁴ Un'altra soluzione fu data da Menecmo mediante le sezioni coniche. Cf. Loria, Le scienze esatte..., pp.150-153.

⁴⁵ Cf. Loria, Le scienze esatte..., pp. 94-98.

⁴⁶ I vari passaggi mediante figure sono resi in modo molto chiaro nell'edizione del Menone tradotto e commentato da G. Reale in Platone. Tutti gli scritti, a c. di G. Reale, Bompiani, Milano 2000, pp. 968-969. Inoltre cf. C. Cellucci, Le ragioni della logica, Laterza, Roma-Bari 1998, pp. 279-283.

⁴⁷ K. Von Fritz, Grundprobleme der Geschichte der antiken Wissenschaft, W. de Gruyter, Berlin-New York, 1971, pp. 564-567.

⁴⁸ Cf. Timpanaro Cardini, Pitagorici. Fasc. II, pp. 383-387.

⁴⁹ Euclid, The Thirteen Books of the Elements. Vol. II, Books III-IX, translated with introduction and commentary by T. L. Heath (1908), Dover Publications, New York, 1956 (rist. anast. della II ed. Oxford University Press 1925), p. 112.

⁵⁰ Cf. Euclide, Elementi, a c. di A. Frajese e L. Maccioni, UTET, Torino, 1970, pp. 291-292.

⁵¹ Ibid., p. 300.

⁵² Trascrivo la traduzione di Frajese-Maccioni in Euclide, Elementi, p. 299.

⁵³ Riporto la citazione di Galilei adoperata da E. Giusti, Euclides reformatus. La teoria delle proporzioni nella scuola galileiana, Bollati Boringhieri, Torino 1993, p. 65. Sulla critica di Galileo alla definizione eudossiana-euclidea cf. in particolare Ibidem, pp. 65-68 e A. Frajese, Galileo matematico, Studium, Roma 1964, pp. 38-52.

⁵⁴ Oltre all'uso di frazioni numeriche (quindi rapporti tra numeri), sappiamo che furono fatti tentativi per la misura indiretta di grandezze, esprimendo poi il valore cercato in un rapporto numerico. Cf. A. Mieli, La scienza greca. I Prearistotelici, Libreria della Voce, Firenze 1916, 12-14. Cf. anche F. Hultsch cit. in Heath, Greek Math., p. 22.

⁵⁵ La def. 4 è il cosiddetto "postulato di Archimede".

⁵⁶ Entra in gioco l'infinito: questo è inevitabile nel caso di grandezze incommensurabili. Ricordiamo che il libro V si propone di unificare la teoria delle proporzioni per grandezze commensurabili e non. Non serve forse ricordare i problemi connessi all'infinito per la matematica greca.

⁵⁷ Frajese definisce Eudosso l'"imbrigliatore dell'infinito", Euclide, Elementi, p. 931.

⁵⁸ Per una breve e chiara esposizione del metodo di esaustione cf. G. Basti, Filosofia della natura e della scienza. Vol. I, Lateran University Press, Roma 2002, p. 57 ss..

⁵⁹ Cf. anche Euclide, Elementi, pp. 931-936 n. 2. Vogliamo aggiungere che sembra che già Democrito avesse anticipato l'esaustione, nel procedimento che lo portò al calcolo del volume del cono. Cf. Giustini, Da Euc. ad Hilb., pp. 59-64.

⁶⁰ L'esperimento geometrico sullo schiavo serve infatti per dimostrare la dottrina dell'anamnesi (Men. 81 e ss.).

⁶¹ Cf. Cambiano, Il metodo..., p. 143.

⁶² È Proclo ad informarci, infatti, che il metodo per analisi sarebbe stato insegnato a Leodamante da Platone, come si dirà più avanti.

⁶³ Cf. V. Hösle, I fondamenti dell'aritmetica e della geometria in Platone, Vita e Pensiero, Milano 1994, pp. 131 ss.. La Repubblica risale infatti al 374 a.C circa; in quel tempo Eudosso aveva intorno ai 26 anni, mentre i suoi lavori di assiomatizzazione (della teoria delle proporzioni) si fanno risalire alla sua maturità, durante il secondo soggiorno ad Atene (368 a.C). Non dovrebbe servire ricordare che Platone usa il metodo per ipotesi, che è una forma del metodo analitico (cf. Cellucci, Le ragioni..., pp. 272-279).

⁶⁴ Il termine polymathia compare la prima volta in Eraclito, che ne parla con tono disprezzante: "sapere molte cose non insegna ad avere intelligenza" (fr. 40), motivo per cui scredita intellettuali del peso di Omero (fr. 56), Pitagora (fr. 81), Esiodo (fr. 57, 106).

⁶⁵ Giamblico, che ci informa su questa notizia, è decisamente contraddittorio, qualora dice che Ippaso fu cacciato dalla comunità o messo a morte dagli dei per aver scoperto l'incommensurabilità, oppure per aver inscritto il dodecaedro in una sfera o semplicemente perché fu il primo a essere conosciuto per certe scoperte quando fino ad allora venivano tutte attribuite a Pitagora (D.-K. 18 A 4).

⁶⁶ Cf. Heath, Gr. Math., pp. 144-149.

⁶⁷ Per un'esposizione esaustiva dei metodi di questi pensatori cf. Loria, Le scienze esatte..., pp. 80-105.

⁶⁸ Sul metodo che Democrito avrebbe seguito i pareri degli studiosi sono discordi. Cf. Giustini, Da Euc. ad Hilb., pp. 61 ss..

⁶⁹ Prendiamo ad esempio la biologia. Di fronte ai fenomeni biologici gli antichi cominciarono a chiedersene le cause e le dinamiche. È risaputo che Anassimandro formulò una sorta di teoria evolutiva secondo la quale gli esseri umani "nacquero dai pesci e furono nutriti come gli squali" (D.-K. 12A30), mentre Empedocle preferisce pensare ad una genealogia in quattro fasi in cui comunque tutti gli esseri viventi nascono dalla terra (D.-K. 31A72). Così come ci si interrogava sul fenomeno della riproduzione: Eraclito (D.-K. 22A19), Alcmeone (D.-K. 24A15), Parmenide (D.-K. 28B18). Ma potremmo parlare di meteorologia e redazioni di calendari, con Talete (D.-K. 11A19), Anassimandro (D.-K. 12A23), Empedocle (D.-K. 31A63); di storiografia con Ecateo di Mileto; di astronomia, con i modelli elaborati nella cosiddetta Scuola di Mileto (D.-K. 11A12-15; 12A11; 13A20), con i Pitagorici, con Anassagora (D.-K. 59A5).

⁷⁰ È questa la tesi ampiamente sviluppata da G. E. R. Lloyd, La scienza dei Greci, tr. it. di A. Salvatori, Laterza, Roma-Bari 1978. Lloyd sottolinea l'uso critico della ragione dei primi pensatori greci in contrapposizione al pensiero mitico. A questo proposito cf. anche L. Rossetti, Se sia lecito incolpare gli Dei (da Omero ad Aristotele) in Studi di Filologia classica in onore di Giusto Monaco, Università di Palermo, Palermo 1991.

⁷¹ D.-K. 21 B 15. Senofane credeva anche nella progressività del sapere (D.-K. 21 B 19).

⁷² Si trattava cioè di mettere insieme il calendario solare con quello lunare. Il primo nome di scienziato che tentò l'impresa è quello di Cleostrato, che ideò l'ottaeride (ciclo ottennale costituito da cinque anni di 12 mesi e tre anni intercalari di 13 mesi, D.-K. 6B4); visto i limiti di quest'ultimo, molti astronomi greci elaborarono sistemi di correzione (ciclo di 59 anni di Enopide di Chio, ritoccato poi da Filolao di Taranto; il ciclo di 82 anni solari con 102 lunazioni di Democrito di Abdera) fino a giungere al ciclo di 19 anni di Metone. Andrebbe indagata la notizia secondo cui Eraclito propose un grande anno di 10.800 anni (D.-K. 22 A 13). Cf. G. Schiaparelli, Sui Parapegmi o Calendari astro-metereologici degli Antichi, Annuario Meteorologico Italiano 1892 in Scritti sulla storia dell'astronomia antica, Mimesis, Bologna 1925 e E. J. Bickermann, La cronologia nel mondo antico, La Nuova Italia, Firenze 1963.

⁷³ Cf. Tannery, La geom. gr., pp. 90 ss..

⁷⁴ Netz, La mat. nel V sec., p. 763.

⁷⁵ Cf. M. Kline, Storia del pensiero matematico, Einaudi, Torino 1999, Vol. I, pp. 44-47; C. B. Boyer, Storia della matematica, ISEDI, Milano 1976, p. 88; ed altri.

⁷⁶ Szabó, Les débuts..., pp. 237-238.

⁷⁷ Netz, La mat. nel V sec., p. 757.

⁷⁸ L. Geymonat, Storia del pensiero filosofico e scientifico, Ed. Garzanti, Milano 1970, Vol. I, p. 54: Geymonat elogia l'Eleate per "aver posto in primo piano il problema della verità del linguaggio e del pensiero, il problema della "via", cioè del metodo, che linguaggio e pensiero dovevano percorrere per giungere alla realtà".

⁷⁹ L. Rossetti, Parmenide e il "saper di sapere" in Discorsi per Giuseppe Martano, Napoli 2002, p.155.

⁸⁰ Ibid., p. 158.

⁸¹ Parmenide di Elea, Poema sulla natura, a c. di G. Cerri, p. 76. In particolare nell'ampia introduzione Cerri contestualizza il Poema tra le opere contemporanee e dimostra come la parte dedicata ai risultati della scienza non è che un resoconto da leggere alla luce di quanto detto prima, e dunque nella consapevolezza che l'esperienza è un punto di partenza necessario ed imprescindibile.

⁸² Faccio riferimento alle pagine antologiche di P. Curd, The Legacy of Parmenides. Eleatic Monism and Later Presocratic Thought, Princeton (New Jersey) 1998, riportate e tradotte da Cerri nella sua edizione di Parmenide, Poema sulla natura, pp. 124-126.

⁸³ Abbondante è la letteratura che ha trattato in maniera più o meno approfondita la figura e i paradossi di Zenone. In particolare segnaliamo però G. Colli, Zenone di Elea, Adelphi, Milano 1998.

⁸⁴ Va notato che prima di Melisso non esiste un linguaggio specifico per l'ontologia e la metafisica; per di più Melisso è il primo a scrivere in prosa.

⁸⁵ O almeno per quanto mi è finora pervenuto. Al massimo viene citato di passaggio, accanto a Parmenide e Zenone, per precisare che faceva parte della stessa corrente filosofica come in Loria, Le scienze esatte..., p. 56.

⁸⁶ Sono stati fatti vari tentativi per sistemare i frammenti di Melisso, non solo dai moderni (Covotti, Mullach, Diels, Reale, Vitali) ma anche dagli antichi (Aristotele, Simplicio, Anonimo del de M X G, i dossografi). L'ordine con cui leggerli non è indifferente a ciò che Melisso avrebbe voluto comunicare. Cf. R. Vitali, Melisso di Samo. Sul mondo o sull'essere, Argalia, Urbino 1973, pp. 91-111.

⁸⁷ Mi attengo alla successione e traduzione dei frammenti di Vitali, Melisso di Samo... .

⁸⁸ Ho approfondito il ruolo di Melisso nell'invenzione del linguaggio della scienza, ovvero nell'invenzione di una modalità per cercare e comunicare ciò che è certo nella comunicazione presentata al convegno dell'I.S.H.R. tenutosi a Madrid nel luglio 2003 con una comunicazione dal titolo "Comunicare il sapere certo: Melisso di Samo".

⁸⁹ Sul rapporto tra logica e dimostrazione geometrica citiamo lo studio F. Bellissima - Paolo Pagli, La verità trasmessa, Sansoni, Firenze 1973.

⁹⁰ Quest'ultima questione avrà una certa importanza in Aristotele, quando in De interpretatione (17b16 ss.) e Topici (109a3 ss.) il filosofo formula le leggi per rapportare proposizioni particolari e universali, ovvero il quadrato logico. Cf. I. M. Bochenski, Ancient Formal Logic, North-Holland Publishing Company, Amsterdam 1968, pp. 27-29 e 37-38; M. Malatesta, La logica delle funzioni. Strumenti per un'indagine transculturale. Vol I. Logica dei predicati, delle classi e delle relazioni, Millennium, Roma 2000, pp. 15-20.

⁹¹ Sull'argomento cf. V. Sainati, La matematica della Scuola Eudossiana e le origini dell'apodittica aristotelica in "Atti del Convegno di Storia della Logica" tenutosi a Parma 8-10 ottobre 1972, Liviana Editrice, Padova 1974.

⁹² Come vuole dimostrare F. Franciosi, Sulle origini del metodo assiomatico-deduttivo nella matematica greca in "Homonoia" 1969 pp. 37-57, p. 37: "riteniamo che [il metodo assiomatico-deduttivo] nacque in seguito a un'improvvisa svolta del pensiero antico, nessuno ci dice esplicitamente quando e per opera di chi questa sia avvenuta".

⁹³ Cf. Cambiano, Il metodo...; E. Berti, L'analisi geometrica della tradizione euclidea e l'analitica di Aristotele in La scienza ellenistica. Atti delle tre giornate di studio tenutesi a Pavia dal 14 al 16 aprile 1982, a c. di G. Giannantoni e M. Vegetti, Bibliopolis, Roma 1984, pp. 93-127; Russo, La rivoluzione..., pp. 190-195; J. J. Sanguineti, Scienza aristotelica e scienza moderna, Armando Editore, Roma 1992; e altri.

⁹⁴ Chiaramente ciò non significa che il contenuto "filosofico" sia uguale. Ad esempio Aristotele ricorre spesso al termine "assioma" per indicare i principi comuni, mentre in Euclide tale termine non è usato.

⁹⁵ Cf. J. Lukasiewicz, Aristotle's Syllogistic from the standpoint of modern Formal Logic, Oxford at the Clarendon Press, London 1957, p. 88.

⁹⁶ Cf. Phys. IV 1.

⁹⁷ Cellucci, Le ragioni..., pp. 291 ss..

⁹⁸ La complessità della teoria con cui Aristotele si rappresenta il rapporto tra la memoria, l'io e le immagini prodotte è comunque un argomento ancora molto discusso. Per una introduzione al problema si legga J. Annas, La memoria e l'io in Aristotele (1992) in Aristotele e la conoscenza, a cura di G. Cambiano e L. Repici, LEI, Milano 1993, pp. 119-144.

⁹⁹ Cf. M. Mignucci, La teoria aristotelica della scienza, Sansoni Ed., Firenze, pp. 301-315; D. W. Hamlyn, L'epagoge aristotelica (1976) in Aristotele e la conoscenza, a cura di G. Cambiano e L. Repici, LEI, Milano 1993, pp. 263-285.

¹⁰⁰ Cf. Aristotele, Organon, a c. di G. Colli, Adelphi, Milano 2003, p. 905 comm. a 85a1.

¹⁰¹ Cellucci, Le ragioni..., pp. 122-134.

¹⁰² Basta pensare ai primi tre postulati di Euclide.

¹⁰³ Sono quelli che Tommaso chiamerà principi quoad omnes (In Post. An. I v 50 [7]), dotati di una autoevidenza resa tale dall'intelletto in atto. Tale forma di "evidenza" non visiva può in qualche modo rimandare alla conoscenza come azione interiorizzata di Piaget, senza però sfociare nel comportamentismo (cf. J. Piaget, L'epistemologia genetica, Laterza, Roma-Bari 1983). Questa conoscenza non visiva sembra rievocare la centralità con cui Aristotele considera il "tatto" e la percezione della materia sensibile nella costituzione della conoscenza; ad esempio in De an. B 12 424b10-12: "sui corpi agiscono non già la luce e il buio, né il suono e l'odore, ma gli intermediari in cui essi si trovano". Si tratta chiaramente di un problema che andrebbe adeguatamente indagato.

¹⁰⁴ Le "altre possibilità" sono tutte quelle tracce di geometria non-euclidea presenti nel corpus aristotelicum e notoriamente fatte emergere da I. Toth, Das Parallelen-problem in "Corpus Aristotelicum" in "Archive for History of Exact Sciences" 4-5 1967 ; I. Toth, Aristotele e i fondamenti assiomatici della geometria. Prolegomeni alla comprensione dei frammenti non-euclidei nel "Corpus Aristotelicum" nel loro contesto matematico e filosofico, a c. di G. Reale, tr. it. di E. Cattanei, Vita e Pensiero, Milano 1997 (l'opera è stata appositamente composta per la collana Temi metafisici e problemi del pensiero antico. Studi e testi., n. 56).

¹⁰⁵ I risultati della mia ricerca sull'induzione aristotelica sono esposti in F. Marcacci, L'approccio all'Assoluto e le entità matematiche in Aristotele e in Euclide. Analisi storico-genetica e confronto tra le due assiomatiche, Theses ad Doctoratum in Philosophia, PUL, Roma 2004. Per il momento rimando ai risultati di Basti (1997): G. Basti, L'approccio aristotelico-tomista alle aporie dell'induzione in G. Basti - F. Barone - C. Testi (Eds.), Il fare della scienza. I fondamenti e le palafitte, Padova, 1997 pp. 41-95.

¹⁰⁶ Non solo nella scienza, ma anche nella filosofia. Si pensi per esempio all'Ethica more geometrica demonstrata di B. Spinoza.
 
 

Flavia Marcacci si è laureata in Filosofia antica presso l'Università di Perugia, integrando gli studi filosofici con dei corsi seguiti presso la Facoltà di Scienze matematiche, fisiche e naturali. Conseguirà il Dottorato in Filosofia della Scienza con tesi sull'assiomatica da Aristotele ad Euclide presso la Facoltà di Filosofia della Pontificia Università Lateranense di Roma nel corso dell'ottobre 2004. Svolge inoltre attività di Tutor per il corso di Informatica e Informatica generale presso la Facoltà di Scienze della Formazione di Perugia. Ha pubblicato diversi articoli riguardanti la matematica e le scienze degli antichi Greci.

flavia.marcacci@virgilio.it